社会人がフーリエを勉強する話 ①フーリエ級数展開

こんにちは。今回は、社会人がフーリエ級数展開を勉強する話です。
フーリエ級数展開とフーリエ変換について学んでおり、今回はその前半である「フーリエ級数展開」までをまとめます。

なぜフーリエを勉強するのか？

データサイエンスや人工知能（AI）といった分野でフーリエ解析は重要なツールとなっています。
例えば、以下のような場面でフーリエの知識が役立ちます。

フーリエ解析は、データを異なる周波数成分に分解する手法なので、時系列データや波形の解析において強力な武器になります。
これからの時代、データを扱う職業に就いている人は、フーリエ解析の基礎を理解しておくと、仕事の幅が広がるかもしれません。

フーリエ（Joseph Fourier）は、18世紀のフランスの数学者です。彼は熱伝導の研究をしている中で、「あらゆる周期関数は、三角関数の和で表現できるのでは？」という発想に至りました。
これがフーリエ級数展開の出発点となり、その後のフーリエ解析やフーリエ変換の基礎となりました。

フーリエ級数展開とは、周期的な関数を正弦波（サイン関数）と余弦波（コサイン関数）の和で表す手法です。
例えば、音声や画像の波形を分解すると、基本的な正弦波や余弦波の組み合わせで成り立っていることがわかります。

フーリエ級数展開の一般的な式は以下のようになります。

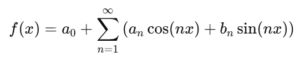
ここで、やはフーリエ係数と呼ばれ、元の関数の形によって決まります。
この展開を使うことで、どんなに複雑な周期関数も三角関数の組み合わせとして表現できるというのが、フーリエ級数の強力なポイントです。

例えば、角ばった波（矩形波）やのこぎり波をフーリエ級数で展開すると、無限個の三角関数の和で表されることが分かります。

社会人が独学で数学を学ぶのはなかなか大変ですが、幸いなことに、今は無料で高品質な授業動画がたくさんあります。
今回の勉強では、YouTubeの「山口大学堀田先生」の講義動画を活用しました。

この動画は、iPadを使って板書をしながら説明するスタイルです。手書きの説明があるため、黒板の授業のように理解しやすくなっています。

フーリエ級数展開の授業は全27回のうち18回まで視聴しました。
三角関数の復習から始まり、実際のフーリエ級数展開の計算まで丁寧に解説されているので、数学が苦手な人でも学びやすい内容になっています。

個人差はあると思いますが、私はこの講義を非常にわかりやすいと感じました。
特に良かったポイントは以下の通りです。

フーリエ級数をしっかり理解するためには、実際に手を動かして計算することが大切なので、この授業はとても役に立ちました。

今回は、フーリエ級数展開について勉強した内容を紹介しました。
社会人でもYouTubeなどを活用すれば、大学の授業と同じレベルの知識を得ることができると実感しました。

次回は、フーリエ変換について勉強した後の感想をまとめる予定です！
フーリエ級数展開が「周期的な関数の分解」だったのに対し、フーリエ変換は「非周期関数を周波数成分に分解する」手法です。

引き続き学んでいきますので、次回もお楽しみに！