こんにちは。今回も引き続き、社会人がフーリエ解析を勉強する話です。
前回はフーリエ級数展開を学びましたが、今回はその後半としてフーリエ変換と逆フーリエ変換を学びました。
前半で扱ったフーリエ級数展開は、周期的な関数を三角関数の和として表す手法でした。一方、今回のフーリエ変換は、非周期関数を周波数成分に分解するための手法になります。
では、フーリエ変換とは何なのか、そしてなぜ社会人でも学ぶ価値があるのかについて紹介していきます。
フーリエ変換とは?
フーリエ変換は、関数を時間領域から周波数領域へ変換する数学的手法です。
具体的には、ある関数 f(t)をフーリエ変換することで、周波数ごとの成分 F(ω) を得ることができます。フーリエ変換の一般的な式は以下の通りです。
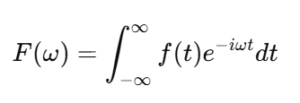
ここで、
- f(t)は時間領域での関数(例:音声、画像、電気信号など)
- は周波数領域での関数(どの周波数成分がどの程度含まれているかを示す)
- は複素指数関数(オイラーの公式を利用)
つまり、フーリエ変換を使うことで、ある関数がどの周波数成分を持っているのかを分析できます。
例えば、音声データをフーリエ変換すると、「どの周波数の音がどれくらい含まれているか」が分かり、ノイズ除去や音声認識に活用できます。
逆フーリエ変換とは?
フーリエ変換で時間領域から周波数領域に変換したものを、再び時間領域に戻す手法を逆フーリエ変換といいます。
逆フーリエ変換の式は次のようになります。
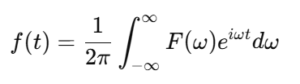
この式を使うことで、フーリエ変換で分解した周波数成分から元の関数を復元することができます。
なぜフーリエ変換を勉強するのか?
社会人がフーリエ変換を学ぶ意義は、データ処理やエンジニアリングの現場で頻繁に使われるからです。
具体的な社会での利用方法
-
音声処理・音楽解析
- MP3やWAVなどの音声データ圧縮
- ノイズ除去(不要な周波数成分をカット)
- 音声認識(周波数ごとの特徴を抽出)
-
画像処理
- JPEG圧縮(フーリエ変換の類似技術である離散コサイン変換を使用)
- エッジ検出やぼかしフィルターの設計
-
通信・信号処理
- 4G/5Gの通信技術(OFDM: 直交周波数分割多重方式)
- 無線通信の周波数分布の解析
-
医学・脳波解析
- MRI(磁気共鳴画像)のデータ解析
- EEG(脳波)の周波数解析
このように、フーリエ変換は私たちの身近な技術に広く使われています。
特に、データサイエンス・機械学習・AIを学ぶ人にとっては、フーリエ変換の基礎を理解することで時系列データ解析などがスムーズになります。
どうやって勉強したか?
前半と同じく、YouTubeの**「山口大学 堀田先生」の講義動画**を使いました。
授業動画について
- 全30本程度の動画(フーリエ級数+フーリエ変換)
- 1つの動画は20分程度 → 社会人でも区切りながら学習しやすい
- 積分計算を丁寧に説明(部分積分も含めて解説)
- 矩形波などの具体例を使って解説
フーリエ変換は積分の計算が多くなりますが、講義動画では手を動かしながら計算を行うので、数式の理解がしやすかったです。
勉強してみた感想
フーリエ級数とフーリエ変換を合わせて約30本の動画を見終えましたが、全体的にとても分かりやすかったです。
特に良かった点は:
- 短時間の動画なので、社会人でも無理なく学習できる
- 積分計算が丁寧で、数学に自信がなくても理解しやすい
- 具体的な例(矩形波や信号処理など)が多く、実践的な知識が身につく
フーリエ変換の計算自体は少し大変ですが、実際に手を動かして計算すると理解が深まります。
また、フーリエ変換は数学だけでなく、データ分析や信号処理の実務にも応用できるので、勉強してよかったと感じています。
次に勉強する内容
今回のフーリエ解析の勉強を通じて、数学の基礎力が重要だと改めて感じました。
山口大学の堀田先生の動画には、線形代数や微積分の講義もあるので、大学数学の基礎を学びたい方にはとてもおすすめです。
そして、筆者は次に複素解析を勉強しようと思っています!
フーリエ変換では複素数を多用するので、より深く理解するために複素関数の微分・積分や留数定理などを学ぶ予定です。
数学の勉強は奥が深いですが、社会人でも時間を工夫すればしっかり学べるので、今後も継続していきたいと思います!

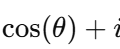
コメント