こんにちは!今回は、社会人が大学数学を勉強する体験記として「複素解析」に挑戦した話をお届けします。仕事や日常生活の合間を縫って、独学で複素解析を学ぶことは決して簡単ではありませんが、意外と楽しみながら進められています。
複素解析とは
まず、複素解析とは何かを簡単に説明します。
複素解析は、複素数(実数と虚数を含む数)を使った関数の解析を行う数学の一分野です。複素数は、実数 と虚数 を使って の形で表されます。ここで は虚数単位で、 i^2=-1です。
複素解析では、複素平面上で関数を扱い、その微分や積分、写像などを学びます。実数の解析よりも美しく、直感的な結果が得られることが多いのが特徴です。
例えば、有名なコーシーの積分定理や留数定理は、複素解析を理解する上で重要な概念です。これらの定理を駆使すると、実数領域では難しい積分も複素平面上では驚くほど簡単に解けることがあります。
AI・機械学習で複素解析を勉強する理由
一見、複素解析はAIや機械学習と直接関係がないように思えますが、実はさまざまな場面で役立ちます。
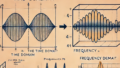
- フーリエ変換やウェーブレット変換
- 信号処理や画像処理で広く使われるフーリエ変換は、複素指数関数を基盤としています。複素解析を理解することで、これらの変換をより深く理解し、効果的に応用できるようになります。
- ニューラルネットワーク
- 一部の研究では、複素数を扱うニューラルネットワーク(複素ニューラルネットワーク)が提案されています。複素解析を学ぶことで、新しいモデルの理解や開発に役立つ可能性があります。
- 最適化手法
- 勾配降下法などの最適化アルゴリズムは、複素関数の微分に基づいた手法も存在します。複素解析の知識は、より高度なアルゴリズムを理解する際にも有用です。
無料の勉強方法
複素解析を学ぶにあたって、もちろん無料で学べる方法を選びました。
今回お世話になっているのは、山口大学の堀田先生のYouTubeチャンネルです。このチャンネルでは、大学レベルの数学を基礎から丁寧に解説してくれています。
- 動画の構成:複素解析は全13回の講義で構成されており、前半と後半に分かれています。各動画は20〜30分程度と短めで、忙しい社会人でも隙間時間に視聴しやすいのが魅力です。
- 視覚的な理解:複素平面上での操作や写像が図解され、直感的に理解しやすくなっています。
現在の進捗
現在、全13回(動画は前半・後半を含めて全26本)のうち、4回目まで学習しました。進捗としては30%ほどです。
ここまでで学んだ主な内容は以下の通りです。
- 複素数の基礎
- 複素数とは何か、複素平面上での表現方法
- 複素数の極形式(極座標を用いた表現)
- オイラーの公式
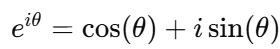
- 美しい関係式を理解
- 複素平面上での操作
- 平行移動、定数倍、反転などの変換
- 指数関数 での変換
感想
学習を進めてみての感想ですが、堀田先生の解説は相変わらずわかりやすいです。基礎から丁寧に教えてくれるので、大学数学から長く離れていた社会人でも無理なくついていけます。
また、1本20〜30分程度の動画なので、通勤時間や休憩時間にサクッと1本学習できる点も嬉しいですね。
特に印象的だったのは、複素平面上での変換を視覚的に確認できたことです。平行移動や反転がどのように図形を変化させるのかを視覚的に理解できると、抽象的な概念がぐっと身近に感じられます。
今後の予定
今後は、複素対数関数(log)や三角関数(sin, cos)の複素平面での挙動を学習する予定です。
また、コーシーの積分定理や留数定理といった、複素解析ならではの強力なツールについても理解を深めていきたいと考えています。
次回は、学習の進捗や、実際に複素解析の知識をどのように応用できるかについてもご紹介する予定です。
興味を持たれた方は、ぜひ一緒に複素解析を学んでみませんか?無料で質の高い教材が手に入る今、挑戦しない手はありません!

コメント