進捗
週末は仕事が休みなので、朝いつものマクドナルドにて勉強
そのあと午前中は近くの体育館で個人開放のバレーボールに行き
午後は娘と公園行ったり三輪車の下見をしたりしました。
第1章 確率モデル
問13,14は回答を見る程度に飛ばしました。
それぞれモンティホール問題、二項定理の証明となっております。
第2章確率変数と確率分布に入っていきます。
問1-3を解きました。
問1
二項分布の確率関数を使った問題です。
(1)
pk=nCk*p^k*(1-p)^(n-k)
pk-1=nCk-1*p^(k-1)*(1-p)^(n-k-1)
があり、pk=●pk-1の形であらわします。
コンビネーションの計算が紛らわしいです。
次にpkの最大値を求めます。
つまりpk-1<pk<pk+1の条件を満たすkを求めます。
(2)
二項定理にそれぞれp,n,kの実数を代入し、計算するだけです。
問2
ポアソン分布の確率関数を使った問題です。
(1)同様、pkとpk-1の確率をそれぞれ式変形して
pk=●pk-1の形であらわします。
(2)
余事象を使います。
1-P(X=0)を求めてその値が0.9より大きくなるλの条件を導きます。
問3
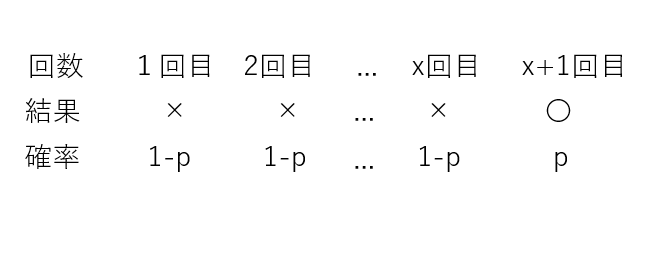
幾何分布の問題です。

X+1が初めて成功した回数なので
Xはそれまでに失敗した回数になります。
p(x)=(失敗の確率^x回)*成功の確率となります。
P(X<k)となるのは上の式の和P(x=0)+P(x=1),..+P(x=k)となるので
等比数列の和を計算すればよいですね。
その値が0.9を超える最小のkを求める。
人にもよりますが入門レベルではない気がします。。

コメント