進捗
今日はいつも通り昼休みに勉強ができました。
第2章確率変数
問7を解きました。
問7
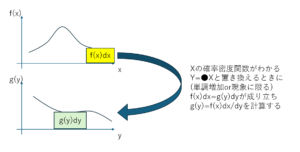
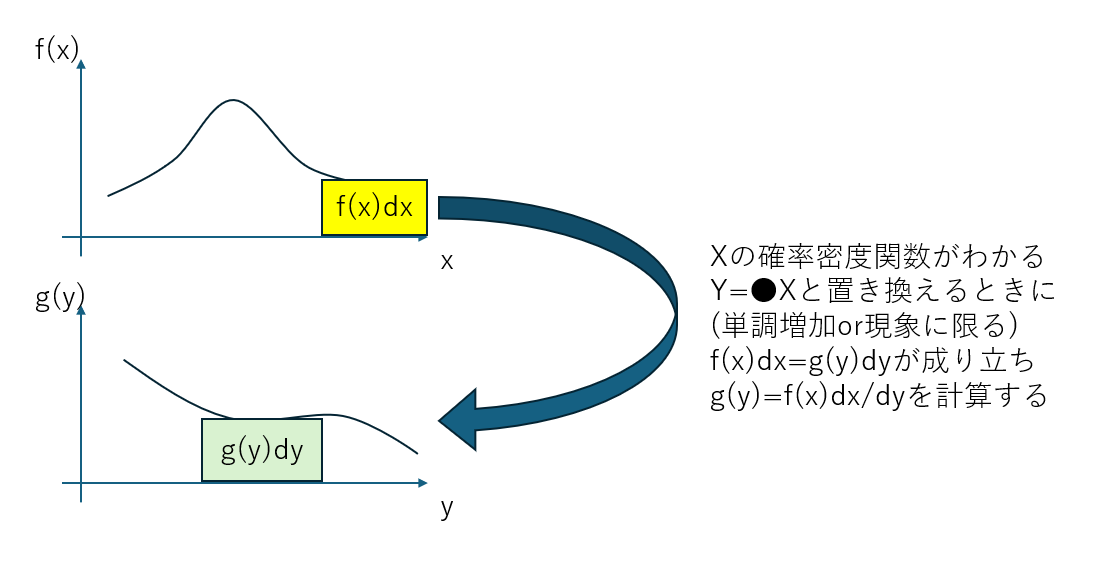
変数変換の問題ですね
(1) Xが正規分布に従うときのY=X^2の確率分布
変数変換は公式がありますが単調増加、減少の時だけ使えるようで今回の場合は基本となる累積分布関数を求めて微分して確率密度関数を作成する方法を使います。
P(Y<y)=P(X^2<y)=P(-√y<X<√y)
f(x)を上記区間で積分し、そのあと微分するのですが微分積分学の基本定理とやらを使い計算します。
Y=|X|の場合も同様です。
(2)
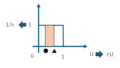
次はU[-1,1]の一様分布ですね、また求めたいのはY=U^2 (0<y<1)なので
同様にP(Y<y)=P(U^2<y)=P(-√y<U<√y)の確率密度を求め,yで微分すれば完成です。
(3)
Y=tanΘとなります。
-π/2<Θ<π/2のときtanΘは単調増加なので公式が使えます。
P(Y<y)=P(tanΘ<y)の計算方法はよくわからないです。
Θ=tan-1(y)とおくとdΘ/dy=1/(1+y^2)となるようで
f(y)=f(Θ)*dΘ/dy=(1/π)*1/(1+y^2)となります。
計算量が多く本日は1問で終了です。

コメント