3章問5
同時確率密度関数から周辺確率、条件付き確率を求める問題
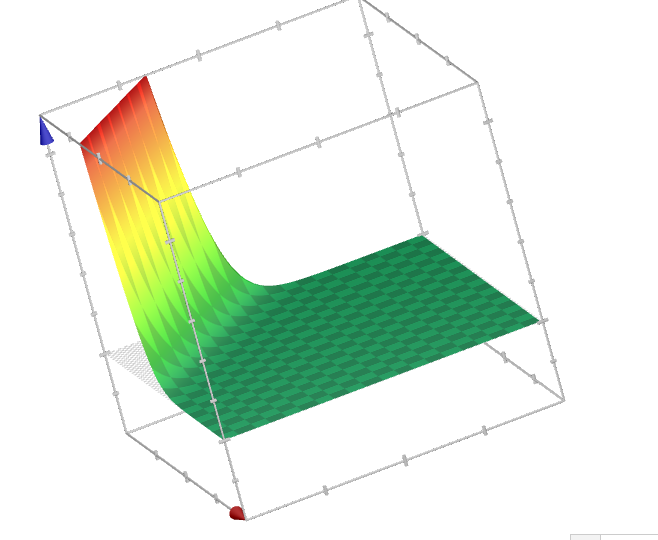
f(x,y)=C*exp(-x-y)
(1)
・Cを求める
Cを求めるにはx,yに対して全区域で積分をする必要があります。
yを優先に考えるとyの積分区間は(0<y<∞)
xの積分区間は(0<x<y)となります。
よって∫∫f(x,y)dxdy=1を計算すればCが求まります。
・Xの周辺分布を求める
f(x,y)をyで積分します。積分区間は(x<y<∞)
xがある値で与えられたときyの積分区間はどうなるかをイメージすればよいかと
fx(x)=∫f(x,y)dy
・Yの周辺分布を求める
f(x,y)をxで積分します。積分区間は(0<x<y)
fy(y)=∫f(x,y)dx
(2)
・Yが与えられたときのXの条件付き確率密度関数を求める
fx|y(x|y)=f(x,y)/f(y)
・Xが与えられたときのYの条件付き確率密度関数を求める
fy|x(y|x)=f(x,y)/f(x)
(3)
P(Y<X+d)=0.9となるdを求める
同時確率密度をx<y<x+dの範囲で積分した結果0.9となるdを求める。
xの積分区間は(0<x<∞)となる
∫∫f(x,y)dydx=0.9
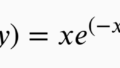
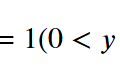
コメント