第3章問2
多項分布の問題
多項分布の確率は下記の通りとなります。
![]()
(1)
例えばX1の周辺分布は
X1とそれ以外(X2,X3,…,Xn)の二項分布になる
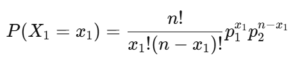
また、例えばX1+X2の周辺分布(X1とX2が出る回数の和)は
(X1,X2)とそれ以外(X3,X4,…Xn)の二項分布になる
![]()
(2)
前段として
X1,X2の同時確率:
X1,X2,それ以外(X3,…,Xn)の多項(三項)分布になる
あとはP(X2|X1)=P(X1,X2)/P(X1)を計算すればよい。
P(X2|X1)つまりX1が与えられた(ある値に決まっている)ときのX2は
二項分布(n-x1,p2/1-p1)となる。
意味合いとしては
試行回数:x1が決まっている為、全体の回数nからx1の出た回数を引く
確率 :x1が決まっている為、全体の確率が1-p1になる
(3)
X1+X2が与えられた(ある値に決まっている)ときのX2の確率は
P(X2|X1+X2)=P(X1,X2)/P(X1+X2)
(X2が決まると自動的にX1が決まる。つまりX1,X2は特定の値に定まることに注意)
つまり二項分布(X1+X2,p2/(p1+p2))となる。
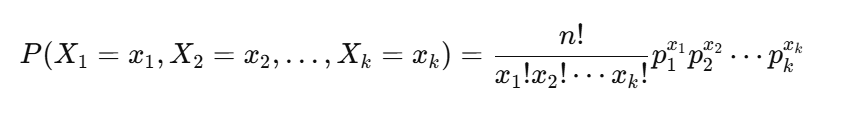


コメント