3章問4
同時確率分布f(x,y)=x*exp(-x(y+1))から周辺分布、条件付き分布を求める問題
積分ができてしまえば問題自体は難しくはないはず。
・Xの周辺分布を求める
yを0<y<∞の範囲で積分していきます。
fx(x)=∫f(x,y)dy
私はChat GPTで積分方法を聞いてu=x(y+1)と置く置換積分を行いました。
・Yの周辺分布を求める
xを0<x<∞の範囲で積分していきます。
コツとしてはガンマ分布(2,(y+1))を式の中に作っていくことです。
fy(y)=Γ(2)/(y+1)^2 {∫(y+1)^2/Γ(2) * x^(2-1)*exp[-(y+1)x]dx}
{}は確率密度関数を全区域で積分しているため1になります。
よってfy(y)=1/(y+1)^2となります。
※Γ(2)=1*Γ(1)=1*1=1
・Yを与えた時のXの条件付き確率を求める
定義通り計算して上記で求めた答えを代入します。
f X|Y(x|y)=f(x,y)/fy(y)
・Xを与えた時のYの条件付き確率を求める
定義通り計算して上記で求めた答えを代入します。
f Y|X(y|x)=f(x,y)/fx(x)
・P(XY>1)となる確率
X(0<x<∞)を先にあたえたときYは積分範囲が1/X<y<∞となります。
よって∫∫f(x,y)dydxを計算していきます。
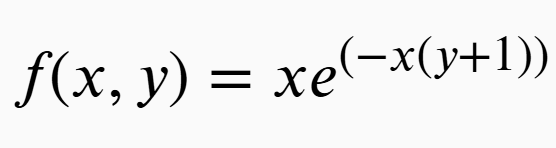


コメント