進捗
今日は午前中、仕事が立て込んでしまい休み時間の開始が遅れてしまい
昼食を取らずに軽く散歩してから30分勉強しました。
働いている以上不確定要素はつきものということで気にせずに問8を解きました。
問8
2章問8
(1),(2)
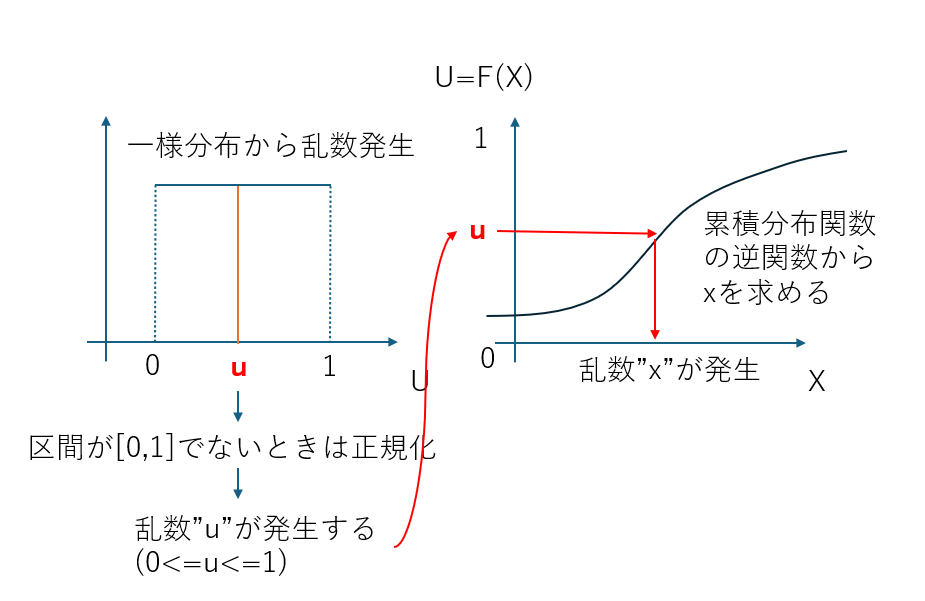
一様乱数Uからとある確率密度関数に従うxの乱数を発生させる方法
解法としては下記の通りとなります。
・確率密度関数から累積分布関数F(x)を求める
・U=F(x)としてx=●の形に書き換える
上記を逆関数法と呼びます。
これでまず一様分布U[0,1]からランダムに値uを発生させて
x=●の●のuに代入してxを生成することが可能になります。
イメージは下図で
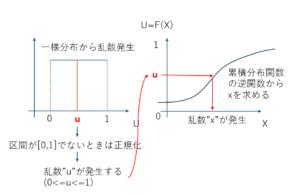
一様分布の定義域と累積分布関数の閾値が同じ範囲になるためこの手法が使われています。
では一様分布[-2,2]のような場合はどうするのかという疑問が浮かびます。
それについては一様分布を変換することで対応できるようで
上記の場合はU’=(U-a)/(b-a)のようにすれば区間が[0,1]になります。
難しく言うと線形写像というものでしょうかね
(この内容が入門かどうかは議論の余地があるかとおもいます。。)
ボリュームが多く本日は以上となります。

コメント