3章問6
一様分布における変数変換の問題
Yは[0,1]区間上の一様分布
Xはyが与えられたとき[0,y]の一様分布となる
(1)同時確率密度関数とXの周辺確率密度関数を求める
・同時確率密度関数は下記のように求めます。
f(x,y)=f(x/y)f(y)
つまりyの確率とyが与えられたときのxの確率を掛けます。
f(v)=1 (0<y<1)、それ以外は0となるのでこれを指示関数Iとします。
f(x|y)=1/y(0<x<y)となります。
よって
f(x,y)=1/y*I
つまり
f(x,y)=1/y (0<y<1)それ以外は0となります。
・Xの周辺確率密度関数を求める
Xがある値(x)のときyの範囲は(x<y<1)となります。
よってf(x,y)を上記xの範囲で積分すればXの周辺確率密度関数が求まります。
fx=∫f(x,y) dy
(2)Z=-logXと置くときのZの確率分布を求める
分布関数から微分をして求めることもできますが
今回は公式を使って求めてみます。
f(z)dz=f(x)dx
x=exp(-z)
dx=-exp(-z)dz
以上より
f(z)=z*exp(-z)となるので
これはガンマ分布Ga(2,1)になります。
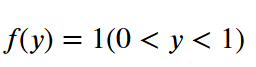


コメント