第2章問12
変更点
今まで解いてきた概要を主にを書いてきましたがこれからは
問題の紹介と自分なりの理解を記載していこうと思います。
問題概要
幾何分布から指数分布を導出する問題です。
理解した内容
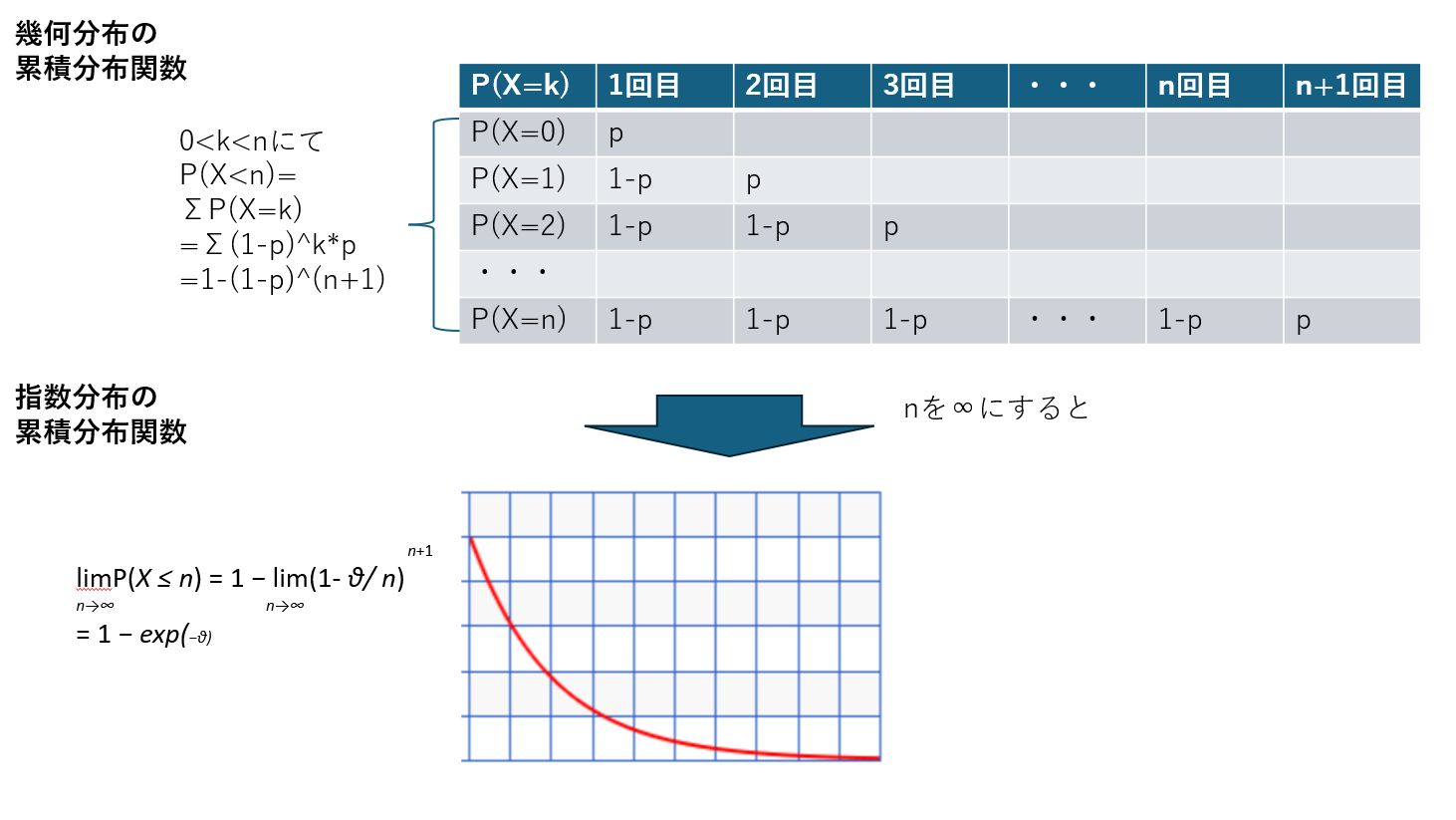
幾何分布の累積分布関数を求めます。
(前回同様失敗した回数をX回とします。)
X=kのとき、つまりk回連続で失敗してk+1回目に成功する確率は
P(X=k)=(1-p)^k*pとなります。
P(X<=n)の確率はP(X=0)+P(X=1)+….+P(X=n)となりますので
シグマを使ってあらわすと
0<=k<=nにて
P(X<=n)=
ΣP(X=k)
=Σ(1-p)^k*p
=1-(1-p)^(n+1)
となります。
ここで問題文に記載してるpをn/Θ
nを極限(+∞)に飛ばすと
lim(P(X<=n))=1-exp(-Θ)となります。
(ネイピア数の計算は割愛)
よって幾何分布の失敗する回数nを∞にとばすと指数分布が導出されます。

本日は以上となります。

コメント