進捗
今日は同僚と昼食を一緒にとりましたので帰宅時にマクドナルドにて勉強しました。
最近は期末テストシーズンや来年の受験に向けて勉強している学生が多いので刺激を受けます。
第2章確率変数
問4-6を解きました。
問4
一様分布の問題
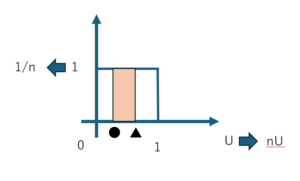
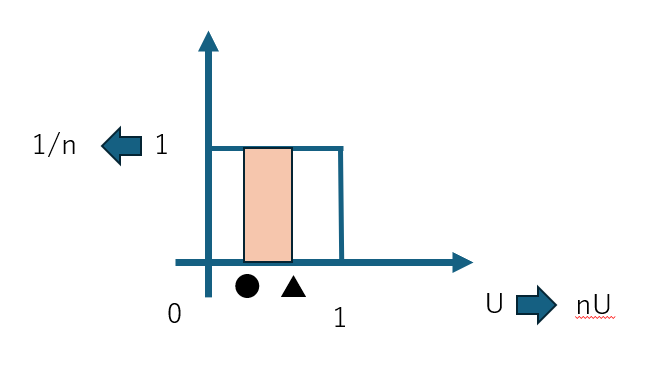
Uが区間[0,1]で一様分布のときはf(u)=1となりますが
nUのときはf(u)=1/nとなります。
図でも説明できますが回答では以下の方法でした。
X=[nU]=kとおきP(X=k)の確率を求める。
K<=nU<k+1の不等式から●<U<▲の形を作り、一様分布から面積を求める。
問5
指数分布の問題
先ほど同様X=[Y]=kとおくと
[Y]の範囲はk<=Y<k+1となります。
Yは指数分布なのでλexp(-λy)を上記の区間で積分すればP(X=k)の確率分布が求められる
問6
正規分布の問題
(1),(2)
Xが正規分布に従っているのでZ=(X-μ)/σと置きます。
P(X>=μ-c)はZのXにμ-cを代入したP(Z>=(μ-c-μ)/σ)と同じになります。
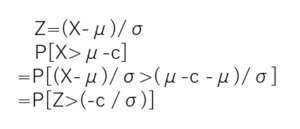
(3)
期待値、分散の性質を利用すると
Xが(μ,σ^2)の正規分布に従うとき
aX+bは(aμ+b,a^2σ^2)の正規分布に従います。
本日は以上となります。

コメント