進捗
本日も昼休みの時間を使って第2章 問題10,11を解きました。
問10
パレート分布の累積分布関数、平均、分散を求める問題です。
α/(1+x)^α+1の積分ができればあとは基本的な計算問題になるかと思います。
平均、分散は回答ではαの範囲をα>1,α>2のときと定めて発散しない範囲で計算してました。たしか統計検定1級の過去問でも同様の問題があったと思います。
問11
両側指数分布、ラプラス分布の問題です。
1/2*exp(-|x|)で(-∞<x<∞)の範囲でxが動きます。
exp(-|x|)はy軸で対象なので2倍にしてxの積分範囲を(0<x<∞)にできます。
∫exp(-x)dx=1 (0<x<∞)となります。
E[x^2]=∫x^2*exp(-x)dx=Γ(3)となります。
※Ga(3,1)は(1^3/Γ(3))*x^(3-1)*exp(-1*x)となり
確率密度関数なので(x>0)で積分すると1になります。
∫(1^3/Γ(3))*x^(3-1)*exp(-1*x)=1となり
∫x^(3-1)*exp(-1*x)=Γ(3)/1^3=Γ(3)
最後に累積分布関数ですが場合分けが必要です。
(ⅰ) x<0のとき
F(x)=1/2∫exp(u)du (-∞<x<0)
=1/2exp(x)
(ⅱ) x>=0のとき
F(x)=1/2∫exp(u)du (-∞<u<0)
+1/2∫exp(-u)du (0<=u<x)
=1/2+1/2(1-exp(-x))

本日は以上です。
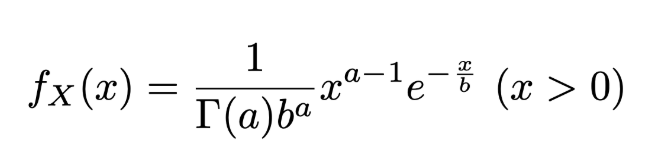


コメント