文系が昼休みに勉強して統計検定1級を受ける⑩

進捗

本日も昼休みの時間を使って第2章 問題9を解きました。

問9

このf(x)はいわゆるロジスティック関数の微分した式となっております。

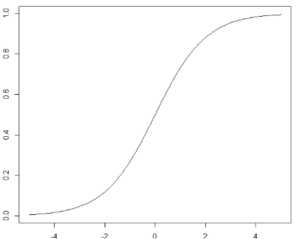
(1)

確率密度関数を示すには以下の2点が必要です。

・f(x)>0 (つまり確率がマイナスにならないよ)

・∫f(x)dx=1 (つまりxの全区間での積分が1になる)

乱数生成については昨日のブログをご参考ください。

(2)

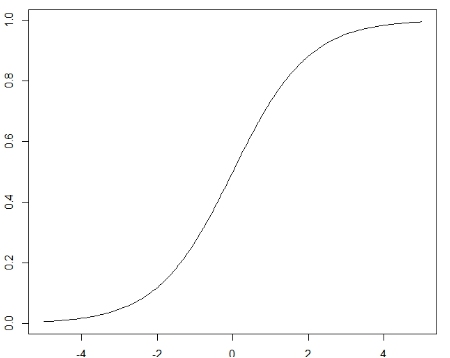
Y=|X|とおいたときのYの確率密度関数を求めます。

F(Y)=P(Y<y)=P(|x|<y)=P(-y<x<y)と変形していきます。

xの確率分布は問題文にありますのでそれを上記区間で積分すればYの累積分布関数、

さらにyで微分するとYの確率密度関数が出てきます。

微分積分の詳細は割愛しますがu=1+exp(−t)とおいて置換積分を行う方法があるかと思います。

問題はもう少し進んだのですがブログ記事に起こす時間が限られており本日はここまでとなります。