正規分布の積率母関数と高次モーメントの計算
この記事では、確率変数 X が正規分布
𝑁(𝜇,𝜎2)に従うとき、積率母関数 𝑀𝑋(𝑡)を求め、
それを用いて高次のモーメント
𝐸[𝑋𝑘]を計算し、さらに歪度と尖度を導出する方法を解説します。
0. 正規分布の基本情報
正規分布の確率密度関数は次の形を持ちます:
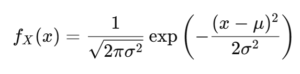
1. 標準正規分布の積率母関数
標準正規分布を用いた積率母関数の導出
標準正規分布(Z = (X − μ)/σ)の積率母関数を求めてから
Xの積率母関数を求めます
標準正規分布Zの確率密度関数は次のようになります:
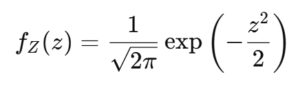
積率母関数
𝑀𝑍(𝑡)は次のように定義されます:
𝑀𝑍(𝑡)=E[exp(tZ)]
これを計算すると:
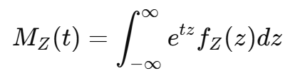
したがって標準正規分布の積率母関数は
𝑀𝑍(𝑡)=exp(t^2/2)
となります。
2. 正規分布の積率母関数
一般の正規分布 X は、標準正規分布 Z を用いて次のように表されます:
X=μ+σZ
積率母関数
𝑀𝑋(𝑡)は次のように定義されます:
𝑀𝑋(𝑡)=E[exp(tX)]
2.1 X を Z で表す
X=μ+σZ を代入すると:
![]()
exp(tμ)は定数なので、期待値の外に出せます。
また、E[e(tσZ)]=MZ(tσ)に標準正規分布の積率母関数
𝑀𝑍(𝑡)=exp(t^2/2)を適用します:
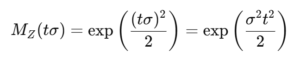
したがって:
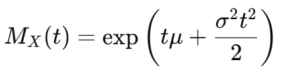
3. 高次モーメント E[Xk]の計算
MX(t) の具体的な導関数を求める
積率母関数の tに関する k 階導関数を用いることで、モーメントを求めます。
上記で求めてたMx(t)についてtに関する導関数を順次計算します。
(3次まで記載してますが4次以降も同様に求められます。)
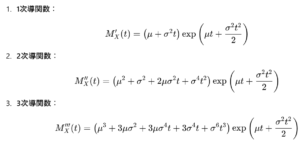
t=0でのモーメント
t=0を代入して、各 E[Xk]を得ます:
- E[X2]=μ2+σ2
- E[X3]=μ3+3μσ2
- E[X4]=μ4+6μ2σ2+3σ4
4. 歪度と尖度の計算
4.1. 歪度(Skewness)
歪度は次の式で計算されます:
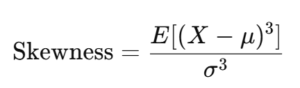
正規分布では E[(X−μ)3]=0であるため
Skewness=0
4.2. 尖度(Kurtosis)
尖度は次の式で計算されます:
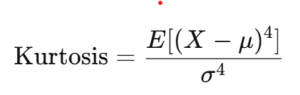
Kurtosis=3
歪度 (Skewness) = 0 から分かること
歪度は、分布の非対称性(左右の傾き)を測る指標です。
- 歪度 = 0 であることは、分布が完全に左右対称であることを示します。
左右対称であるため、平均、中央値、最頻値がすべて一致します
正規分布においては、歪度が 0 であることが特徴であり、他の分布と区別する指標の一つです。
意義:
- 実データが正規分布に近いかどうかを確認する際、歪度が 0 に近いかどうかを確認します。
- 歪度が 0 から大きく外れている場合、分布は非対称であり、正規分布から離れている可能性が高いです。
尖度(Kurtosis)=3 から分かること
尖度は、分布の尾部の厚み(極端な値の発生頻度)を測る指標です。
- 正規分布では、尖度が 3 に固定されています。これは、標準的な「尖り具合」であり、極端な値(外れ値)が出現する頻度が「中庸」であることを示します。正規分布の尖度(3)と比較して:
- 尖度 > 3 の分布は「尖った分布」(leptokurtic)と言い、尾部が重く、極端な値の発生頻度が高いことを示します(例:t分布)。
- 尖度 < 3 の分布は「平坦な分布」(platykurtic)と言い、尾部が軽く、極端な値の発生頻度が低いことを示します(例:一様分布)。
意義:
- 実データの尖度を計算し、3 に近いかどうかを確認することで、正規分布に近いかどうかを判断できます。
- 尖度が大きい場合(> 3)、外れ値がデータに与える影響が大きいため、データ分析やモデリング時に注意が必要です。


コメント