指数分布の概要
統計学や確率論において、**指数分布(Exponential Distribution)**は確率分布の一つで、特に待ち時間や寿命をモデル化する際によく用いられます。この分布は、ランダムな事象が一定の平均速度で発生するプロセスを表します。例えば、あるシステムにおける故障時間、電話が到着する間隔時間、または放射性物質の崩壊時間などです。
指数分布には以下の特徴があります:
- **確率密度関数(PDF)**は、
f(x)=λexp(−λx),x≥0,λ>0 ここで、はパラメータであり、分布の「速さ/頻度」を決定します。 - 平均は 1/λ、分散は 1/λ^2。
- メモリーレス性を持ち、これは過去の事象が未来の確率に影響しないことを意味します。
本記事では、確率変数 X∼Ex(λ) を基に、変数変換を通じて積率母関数や高次モーメントを計算し、さらに歪度や尖度を求める過程を詳しく解説します。
確率変数 Y=λX を用いた解析
確率変数 X∼Ex(λ) を持つ場合、変数変換 Y=λXを行うと、
Y∼Ex(1)に従います。これにより、計算が単純化されます。
1. 積率母関数(MGF)の導出
積率母関数 MY(t)は次の式で定義されます:
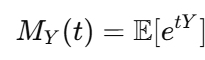
指数分布 Y∼Ex(1) の場合、計算は以下の通りです:
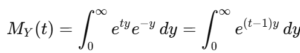
この積分が収束するためには t<1が必要であり、計算結果は次のようになります:
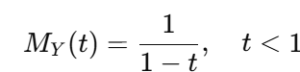
(積率母関数は t>1の範囲では定義されません。物理的な意味では、MGF は確率密度関数に基づく期待値を表しているため、無限大の値を取る状況は確率分布として不適切とされます。)
2. k次モーメントの計算
積率母関数の k次モーメントは、MY(t) のtに関する階微分から求められます:
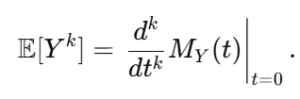
具体的には次のように計算されます:
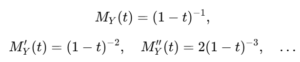
したがって、
E[Y^k]=k!
3. Xの高次モーメント E[Xk]
より、Xのモーメントは以下の関係を用いて計算されます:
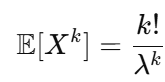
歪度と尖度の計算
1. 歪度
歪度は以下の式で定義されます:
Skewness=E[(X−μ)3]/σ3
指数分布では、μ=1/λ,lambda そして標準化した結果:
Skewness=2
2. 尖度
尖度は以下の式で定義されます:
Kurtosis=E[(X−μ)4]σ4
指数分布では尖度は次のようになります:
結論
指数分布はその単純さと応用の広さから、統計学において非常に重要な分布です。本記事では、変数変換を用いた計算手法を通じて、指数分布の積率母関数、高次モーメント、歪度および尖度を求めました。このアプローチにより、複雑な計算をシンプルに行える方法が示されました。今後の実践的な応用でもぜひ参考にしてください!


コメント