今日から第3章となります。
(2章後半にある※のついた問題は筆者曰くレベルが高いので一周目では飛ばしてよいとのことです。)
第3章問1
条件付き確率の問題です。
四面体が出る目の数でXを和、Yを差とします。
回答と同じようにすべての場合の数を書き出して求めていきましょう。
1回目と2回目で区別が必要なのでその点だけ気を付ければ問題ないです。
(1)
和が4,差が0になる組み合わせは(2,2)だけですね
(2)
和が6になる組み合わせは(2,4),(3,3),(4,2)の3通りです
差が2になる組み合わせは(1,3),(2,4),(3,1),(4,2)の4通りとなります。
(3)
和が4になる条件のもとで差が2になる場合の数を探しましょう。
和が4になるのは(1,3),(2,2),(3,1)の3通り
そのうち差が2になるのは2通り
よって2/3となります。
差が1になる条件のもとで和が5になる場合の数を探しましょう。
差が1になるのは(1,2),(2,3),(3,4),(2,1),(3,2),(4,3)の6通り
そのうち和が5になるのは2通り
よって2/6=1/3となります。
こういった問題を通して条件付き確率のイメージを掴めますね。
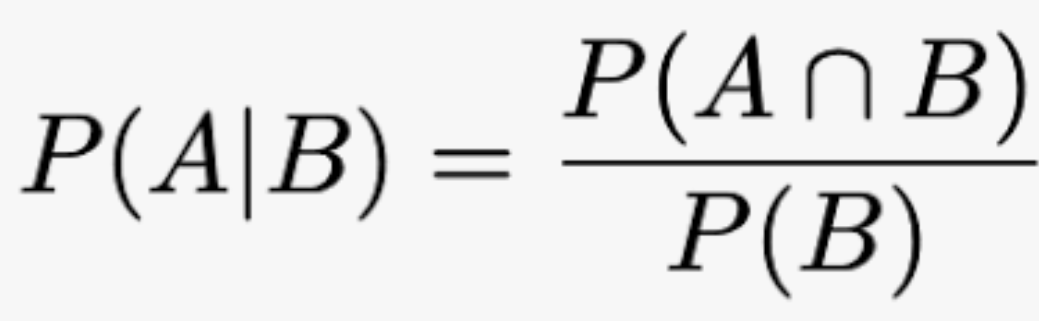


コメント