文系が昼休みに勉強して統計検定1級を受ける㉑(第4章問1-1)

ポアソン分布の概要

ポアソン分布は、単位時間または空間におけるランダムな事象の発生数をモデル化する離散確率分布です。その確率質量関数 (PMF) は次のように定義されます：

ここで、

• $\lambda >0$ は平均発生数を表すパラメータです。

積率母関数の導出

積率母関数 MX(t) は次の定義に基づきます：
MX(t)=E[etX]

ポアソン分布の場合、期待値の計算を直接行うと：

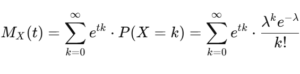
式を整理すると：

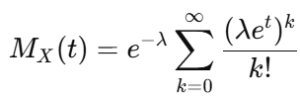
ここで指数関数のテイラー展開を適用すすると
ポアソン分布の積率母関数は次のように与えられます：

積率母関数を用いた E[Xk]の計算

積率母関数 MX(t)を用いることで、期待値 E[Xk]はk階微分後にt=0を代入することで求められます：

E[Xk]=MX(k)(0)

• $k=1$:
  MX′(t)=λeteλ(et−1)より
  MX′(0)=λ
  E[X]=λ
• k=2:
  MX′′​(t)=λet(λet+1)eλ(et−1)より、
  MX′′​(0)=λ+λ2
  E[X2]=λ+λ2
  
• $k=3$:
  MX′′′​(t)=λet(λ2e2t+3λet+1)eλ(et−1)より、
  MX′′′​(0)=λ+3λ2+λ3
  E[X3]=λ+3λ2+λ3
• $k=4$:
  同様に、4階微分を計算すると：
  E[X4]=λ+7λ2+6λ3+λ4 

歪度と尖度の計算

歪度はデータ分布の非対称性を示し、正の値なら右に裾が長く、負の値なら左に長い形状を持ちます。一方、尖度は分布の鋭さを測り、値が大きいほど尖った形状、小さいほど平坦な形状を示します。

ポアソン分布における歪度と尖度は以下のように計算されます：

分散 Var[X]:
Var[X]=E[X2]−(E[X])2=λ+λ2−λ2=λ

歪度 γ1​:
歪度は次の式で計算されます：

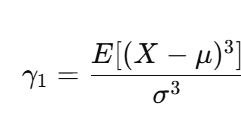
尖度 γ2​:
尖度は次の式で計算されます：

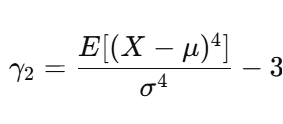
ここで
E[(X − λ)3] =E[X3 − 3X2λ + 3Xλ2 − λ3] = λ3 + 3λ2 + λ − 3λ(λ2 + λ) + 3λ3 − λ3 = λ

E[(X − λ)4] =E[X4 − 4X3λ + 6X2λ2 − 4Xλ3 + λ4]
=λ4 + 6λ3 + 7λ2 + λ − 4(λ3 + 3λ2 + λ)λ + 6(λ2 + λ)λ2 − 4λ4 + λ4
=3λ2 + λ

したがって歪度と尖度はそれぞれ
1/√λ、1/λとなります。